What Are Stock Options in Trading?

Stock options are financial instruments that give you the right, but not the obligation, to buy or sell an underlying asset, usually a stock, at a predetermined price within a specific time frame. These options are traded on various exchanges and can be used for a variety of purposes, including hedging, speculation, and income generation.

The Basics

Long Call Option:

In a long call option, the buyer pays a premium to the seller for the right to buy the underlying stock at a later date. The premium represents the cost of the call option, and it is influenced by several factors:

1. The strike price of the call option, which is the price at which the buyer can purchase the stock.
2. The expiration date of the option, which determines the timeframe during which the buyer can exercise the option.
3. The implied volatility of the stock, as higher volatility can lead to higher option premiums.
4. The current market price of the underlying stock.

Short Call Option:

In a short call option, the seller receives a premium from the buyer in exchange for granting the buyer the right to buy the underlying stock. The premium received by the seller is influenced by the same factors mentioned above, including the current stock price, the strike price, the expiration date, and volatility.

Long Put Option:

In a long put option, the buyer pays a premium to the seller for the right to sell the underlying stock at a later date. Similar to long call options, the premium for a long put is determined by factors such as the stock’s current price, the put option’s strike price, its expiration date, and volatility.

Short Put Option:

In a short put option, the seller receives a premium from the buyer in exchange for granting the buyer the right to sell the underlying stock. The premium received by the seller for a short put is influenced by the same factors, including the current stock price, the strike price, the expiration date, and volatility.

In summary, whether you are buying or selling call or put options, the premium paid or received is a critical component of the option contract’s value. It is influenced by various market factors, and understanding these factors is essential for effective options trading.

Key factors include the current stock price, the option’s strike price, the expiration date, and the level of volatility in the underlying stock.

Types of Stock Options

There are two main types of stock options:

1. Long Call:

A long call gives the holder the right to buy a stock at a set price (strike price) before the option expires. Investors use this when they expect the stock price to rise. The risk is limited to the premium paid, while the profit potential is unlimited if the stock price increases.

2. Short Call:

A short call involves selling a call option, giving the buyer the right to buy the stock at the strike price. The seller earns a premium but risks unlimited losses if the stock price rises, as they may have to sell the stock at a lower price.

3. Long Put:

A long put gives the holder the right to sell a stock at the strike price. It’s used when expecting the stock price to fall. The loss is limited to the premium paid, and profit increases as the stock price declines, with maximum profit if the stock falls to zero.

4. Short Put:

A short put involves selling a put option, giving the buyer the right to sell the stock to the seller. The seller receives a premium but risks losses if the stock price falls, as they may have to buy the stock at a higher price than its market value.

How They Work

1. Long Call:

When you buy a long call option, you’re betting that the stock’s price will rise above the strike price before the option expires. If the stock price increases, you can either sell the option for a profit or exercise it to buy the stock at the strike price, which would be lower than the current market price. The risk is limited to the premium paid for the option, while the potential reward is unlimited as the stock price rises.

2. Short Call:

When you sell a short call option, you’re betting that the stock’s price will stay below the strike price before expiration. If it does, the option will expire worthless, and you keep the premium. However, if the stock price rises above the strike price, you may be forced to sell the stock at the strike price, potentially at a significant loss. The risk in a short call is theoretically unlimited, as the stock price can keep rising.

3. Long Put:

When you buy a long put option, you’re betting that the stock’s price will fall below the strike price before expiration. If the stock price drops, you can either sell the option for a profit or exercise it to sell the stock at the strike price, which would be higher than the current market price. Your risk is limited to the premium paid for the option, while the reward grows as the stock price declines.

4. Short Put:

When you sell a short put option, you’re betting that the stock’s price will stay above the strike price before expiration. If it does, the option will expire worthless, and you keep the premium. However, if the stock price falls below the strike price, you may be forced to buy the stock at the strike price, which could be higher than its current market value, leading to potential losses. The risk is limited to the strike price minus the premium received.

Why Trade Stock Options?

There are several reasons why investors trade stock options:

1. Hedging: To protect against potential losses in stock portfolios.
2. Speculation: To bet on the future price movements of stocks without actually owning them.
3. Income generation: Through strategies like selling covered calls.

Risks Involved

While stock options can offer high returns, they also come with high risks:

• Potential losses: The premium you pay for an option could be lost entirely if the stock doesn’t move in the direction you anticipated.
• Complexity: Options are complex instruments that require a good understanding of the market and a solid trading plan.

Tip: Stock options are versatile financial instruments that offer a range of possibilities for sophisticated investors. However, they are not suitable for everyone due to their complexity and high risk. Before diving into options trading, it’s crucial to educate yourself and possibly consult with a financial advisor.

How Do Stock Options Work?

Stock options are contracts that give you the right, but not the obligation, to buy or sell a stock at a predetermined price within a specific time frame. Let’s explore the mechanics of stock options, how they are priced, and how they can be used in various trading strategies.

The Contract:

A stock option is a contract that involves two parties: the option buyer and the option seller (also known as the option writer). The buyer pays a premium to the seller to acquire the right to buy (call option) or sell (put option) a stock at an agreed-upon price, known as the strike price, within a certain period, up to the expiration date.

Premium and Pricing:

The cost of an option, known as the premium, is determined by several factors, including the stock’s current price, the strike price, the time until expiration, and the stock’s volatility.

Call and Put Options:

• Call options: The holder has the right to buy a stock at the strike price before expiration.
• Put options: The holder has the right to sell a stock at the strike price before expiration.

Exercising Options:

When you exercise a call option, you buy the underlying stock at the strike price. When you exercise a put option, you sell the underlying stock at the strike price. Many options are not exercised but instead traded back in the market, allowing you to realize gains or losses without owning the underlying asset.

Trading Strategies:

Stock options can be used in various strategies, including hedging, speculation, and income generation. Examples include:

1. Hedging: Protecting against potential losses in a stock portfolio.
2. Speculation: Betting on the direction of stock prices without owning the stocks themselves.
3. Income generation: Through strategies like covered calls.

Risks and Rewards:

Options trading can be profitable but also carries significant risks. One of the main risks is the potential loss of the entire premium paid for the option if the stock does not move in the direction you anticipated. Therefore, it’s crucial to understand your risk tolerance and have a well-thought-out trading plan.

Tip: Stock options are complex financial instruments that offer a range of opportunities for those who understand their intricacies. They can be used for hedging, speculating on future price movements, or generating additional income. However, the complexity and risks involved mean that they are not suitable for everyone. Before engaging in options trading, make sure to educate yourself thoroughly and consider seeking advice from financial professionals.

What is the Difference Between Call and Put Options?

In the realm of stock options, two terms you’ll frequently encounter are “call options” and “put options.” Understanding the difference between these two types of options is crucial for anyone interested in options trading. Here’s a breakdown of what call and put options are, how they differ, and how traders can utilize them in various strategies.

Call Options Explained:

A call option is a financial contract that gives the holder the right, but not the obligation, to buy a specific amount of an underlying asset, typically a stock, at a predetermined price (the strike price) within a set time frame. The buyer pays a premium to the seller (or writer) of the option for this right.

When to Use Call Options:

Call options are generally used when you expect the price of the underlying asset to rise. They can be employed in various strategies, including:

1. Speculation: Investors buy call options when they believe the underlying stock’s price will increase. This can be a cost-effective way to benefit from a stock’s potential rise compared to buying the stock outright.

Mathematical Example (Call Option):

• Stock ABC’s current price (S): $50
• Strike price (X): $55
• Premium (C): $3.50
• Time until expiration (T): 90 days
• Risk-free interest rate (r): 0.05 (5%)

You decide to buy a call option with a strike price of $55 for $3.50. Using the put-call parity, you can assess the cost of buying the stock outright versus buying the call option.

Hedging with Call Options:

Hedging involves using options to offset potential losses in other investments. When you short a stock (sell it with the expectation that its price will fall), buying a call option can serve as a hedge, protecting you from significant losses if the stock price increases unexpectedly.

Mathematical Example (Hedging with Call Options):

• Stock XYZ’s current price (S): $60
• Strike price (X): $65
• Premium (C): $3.50
• Time until expiration (T): 60 days
• Risk-free interest rate (r): 0.04 (4%)

Buying a call option in this scenario can help hedge against potential losses in your short position if XYZ’s price rises beyond $65.

Put Options Explained:

A put option gives the holder the right, but not the obligation, to sell a specific amount of an underlying asset at a predetermined price within a set time frame. Like call options, you pay a premium to the option writer.

When to Use Put Options:

Put options are typically used when you expect the price of the underlying asset to fall. They can be used in strategies such as:

1. Speculation: If you anticipate a stock’s price will decline, buying a put option can offer potential profits.
2. Hedging: If you own a stock, buying a put option can protect you from losses if the stock price decreases.

Key Differences Between Call and Put Options:

• Directional Bias: Call options are used when expecting the underlying asset to rise in price, while put options are used when expecting a decrease.
• Rights Conferred: Call options give the right to buy, while put options give the right to sell the underlying asset.
• Risk Profile: The risk in buying a call option is limited to the premium paid, but the potential gain is theoretically unlimited. In contrast, buying a put option limits risk to the premium paid, but the potential gain is capped at the strike price minus the premium.

Tip: Understanding the difference between call and put options is foundational for anyone interested in options trading. While they serve as the building blocks for various complex trading strategies, their basic difference lies in the directional bias and the rights they confer to the holder.

How Can You Make Money with Stock Options?

Stock options offer a versatile way to profit from the financial markets. Whether you’re looking to hedge your portfolio, generate income, or speculate on stock movements, options can be a valuable tool. Here are several ways you can make money with stock options.

Buying Call Options:

One of the most straightforward ways to make money with options is by buying call options. If you expect a stock’s price to rise, you can buy a call option that gives you the right to purchase the stock at a predetermined price (strike price) within a specific time frame.

If the stock price rises above the strike price plus the premium you paid, you can either sell the option for a profit or exercise it to buy the stock at the strike price.

Buying Put Options:

Buying put options is a strategy used when you expect a stock’s price to fall. It gives you the right to sell the stock at a predetermined price within a specific time frame.

Example (Put Option):

• Stock XYZ’s current price (S): $50
• Strike price (X): $45
• Premium paid for put option (P): $3
• Time until expiration (T): 60 days

To calculate the potential profit or loss, use the following formula:

Profit/Loss = max(0, X − S) − P

If the stock price falls below the strike price, your put option becomes profitable, and you can either sell the option for a profit or exercise it to sell the stock at the strike price.

Selling Options:

Selling options involves collecting a premium from the buyer, but it also comes with obligations.

Example (Selling Call Option):

• Stock ABC’s current price (S): $55
• Strike price (X): $60
• Premium received for call option (C): $4
• Time until expiration (T): 45 days

If the option is exercised, you may have to sell the stock at the strike price. Your profit or loss can be calculated using:

Profit/Loss = −max(0, S − X) + C

Covered Calls:

Writing covered calls is a popular strategy when you own the underlying stock.

Example (Covered Calls):

Suppose you own 100 shares of stock DEF, trading at $70 per share. You sell a call option with a strike price of $75 and receive a premium of $3.50. If the option is exercised, you may have to sell your 100 shares at $75 each.

Profit/Loss = (C + X − S) × 100

Cash-Secured Puts:

Selling cash-secured puts involves selling a put option and keeping enough cash to buy the stock if it falls to the strike price.

Example (Cash-Secured Puts):

You sell a put option on stock GHI with a strike price of $45 and receive a premium of $2.50. You set aside $4,500 in cash to potentially buy 100 shares if the option is exercised.

Profit/Loss = P − (X − S) × 100

Spreads:

Options spreads involve buying and selling multiple options simultaneously.

Example (Bull Call Spread):

In a bull call spread, you buy a call option while selling another call option with a higher strike price. Suppose you buy a call option with a strike price of $50 for $3 and sell a call option with a strike price of $55 for $1.

The maximum profit for this spread is the difference in premiums, and the maximum loss is the net premium paid.

Tip: Making money with stock options involves various strategies, each with its own risk and reward profile. Whether you’re buying calls or puts, selling options, or using more complex strategies like spreads, the key to success is understanding the underlying mechanics and risks.

What Are the Risks Involved in Trading Stock Options?

While stock options offer opportunities for profit and portfolio management, they also come with risks. Understanding these risks is essential for successful options trading.

Risk of Losing the Entire Premium:

When you buy an option, you pay a premium for the right to buy or sell a stock at a predetermined price. If the stock doesn’t move in the direction you anticipated, you could lose the entire premium you paid. This is a significant risk, especially for inexperienced traders.

Market Risk:

Like any financial instrument, options are subject to market risks, including volatility and price fluctuations. A sudden market downturn can result in significant losses, especially for options sensitive to market changes.

Complexity and Lack of Understanding:

Options are complex instruments requiring a good understanding of the market, the underlying asset, and the option contract itself. Lack of understanding can lead to poor decision-making and increased risk.

Leverage Risk:

Options offer leverage, meaning you can control a large amount of stock for a relatively small investment. While this can amplify profits, it can also amplify losses.

Time Decay:

Options have an expiration date, and as they approach this date, their value can decay rapidly. This is known as “theta,” and it’s a risk particularly for option buyers.

Assignment Risk

When you sell an option, you take on the obligation to buy or sell the underlying stock if the option is exercised. This is known as assignment risk and can result in unexpected financial obligations.

Tip: Options trading offers opportunities but also comes with significant risks. Understanding and managing these risks are crucial for long-term success in the options market.

Risk Mitigation Strategies

While options trading is risky, there are ways to mitigate these risks:

Education

The more you know, the better you can manage risks. Take the time to educate yourself about options and the markets.

Diversification

Don’t put all your eggs in one basket. Diversifying your options strategies can help spread risk.

Risk Capital

Only trade with money you can afford to lose.

Professional Advice

Consider consulting a financial advisor who can guide you based on your individual financial situation.

Tip: Options trading offers a world of opportunities but also comes with significant risks. Understanding these risks and how to manage them can go a long way in determining your success or failure in the options market.

How Do You Choose the Right Stock Options to Trade?

Choosing the right stock options to trade can be a daunting task, especially for those new to the world of options trading. With a plethora of choices available, how do you narrow down your options to make the most informed decision? Here are several factors and strategies to consider when selecting the right stock options to trade.

Understand Your Objective

Before diving into options trading, it’s crucial to understand your investment objectives. Are you looking to hedge your portfolio, generate income, or speculate on stock price movements? Your objectives will guide your choice of options.

Research the Underlying Stock

The performance of an option is closely tied to its underlying stock. Therefore, it’s essential to research the stock’s fundamentals, technicals, and market sentiment. Look for stocks or etf’s with good liquidity, low bid-ask spreads, and strong fundamentals.

Consider Volatility

Volatility plays a significant role in options pricing. High volatility often leads to higher premiums, making it expensive to buy options. On the flip side, high volatility can also offer higher profit potential. Understanding implied volatility and historical volatility can help you gauge whether an option is overpriced or underpriced.

Expiration Date

Options come with an expiration date, and it’s crucial to choose an option with an expiration that aligns with your trading strategy. Short-term options are more sensitive to price movements but are also subject to rapid time decay. Long-term options are less sensitive to short-term price fluctuations but cost more.

Strike Price

The strike price is the price at which you can buy or sell the underlying stock. Options can be in-the-money (ITM), at-the-money (ATM), or out-of-the-money (OTM), depending on the stock’s current price relative to the strike price. Each has its own risk-reward profile, and your choice should align with your market outlook.

Liquidity

Liquidity is crucial when trading options. Illiquid options can have wide bid-ask spreads, making it difficult to enter or exit trades at favorable prices. Always check the option’s trading volume and open interest before making a decision.

Risk Tolerance

Options trading involves risk, and it’s essential to choose options that align with your risk tolerance. Whether you’re buying or selling options, make sure you’re comfortable with the potential losses.

Diversification

Don’t put all your eggs in one basket. Consider diversifying your options trades across different stocks, sectors, or even asset classes to reduce risk.

Cost and Fees

Be mindful of the costs associated with trading options, including commissions and fees. These costs can eat into your profits, especially if you’re trading frequently.

Tip: Choosing the right stock options to trade involves a careful analysis of various factors, including your investment objectives, the underlying stock, volatility, expiration date, and your own risk tolerance. By taking the time to understand these elements and how they interact, you can make more informed decisions and increase your chances of success in the options market.

What Are the Tax Implications of Trading Stock Options?

Trading stock options can be a lucrative venture, but it’s essential to understand the tax implications that come with it. The tax treatment of options trading can be complex and varies depending on various factors, including the type of options, how long you hold them, and your overall trading activity. Let’s explore the tax considerations you should be aware of when trading stock options.

Short-Term vs. Long-Term Capital Gains

The tax treatment of your options trades depends on how long you hold the options. If you hold an option for one year or less before it expires or you exercise it, any gains are considered short-term capital gains and are taxed at your ordinary income tax rate. On the other hand, if you hold an option for more than one year, any gains are considered long-term capital gains and are taxed at a lower rate.

Tax Treatment for Buyers

If you buy an option and it expires worthless, you can report the premium you paid as a capital loss. If you exercise the option, the premium you paid is added to the cost basis of the stock you acquire, affecting the capital gains or losses when you eventually sell the stock.

Tax Treatment for Sellers

If you write (sell) an option, the premium you receive is not immediately taxed. Instead, it’s recognized when the option is exercised, expires, or you execute an offsetting transaction. If the option is exercised, the premium reduces the cost basis for the stock you buy or sell.

Taxes on Spreads, Straddles, and Other Complex Trades

Advanced options strategies like spreads and straddles have their own tax implications. These can be complex and may require specialized tax advice. Some strategies may trigger the “wash sale” rule, which disallows the capital loss deduction if you repurchase a “substantially identical” investment within 30 days before or after a sale at a loss.

Record-Keeping

Maintaining accurate records is crucial for determining your tax liability. Keep track of all transactions, including premiums paid or received, dates of transactions, and any resulting gains or losses.

Section 1256 Contracts

Some options, like index options, are considered Section 1256 contracts and are subject to different tax rules. Gains and losses from these options are considered 60% long-term and 40% short-term, regardless of the holding period.

Professional Trader Status

If you’re a full-time trader, you might qualify for “trader tax status,” which allows you to deduct trading-related expenses and elect “mark-to-market” accounting, affecting how gains and losses are reported.

Consult a Tax Advisor

Given the complexity of tax rules surrounding options trading, it’s advisable to consult a tax advisor who can provide guidance tailored to your specific situation.

Tip: Understanding the tax implications of trading stock options is crucial for any trader. The tax treatment varies depending on various factors and can be complex. Proper record-keeping and consultation with a tax advisor can help you navigate the tax landscape effectively, allowing you to focus on your trading strategies.

How Do You Read an Options Chain?

An options chain is a crucial tool for anyone involved in options trading. It provides a comprehensive snapshot of all the options available for a particular stock, including their strike prices, expiration dates, and premiums. Knowing how to read an options chain can give you a significant edge in making informed trading decisions. Let’s break down the key components of an options chain and how to interpret them.

What is an Options Chain?

An options chain is a table that displays the various options contracts available for a specific stock or index. It’s usually available on financial websites and trading platforms. The chain is organized by expiration dates and strike prices, making it easier to compare different options.

Long and Short Call Options

Long Call Option

A long call option gives the holder the right to buy the underlying stock at the strike price before or at the expiration date. The holder pays a premium for this right.

Example:

• Stock ABC’s current price (S): $50
• Strike price (X): $55
• Premium paid for the call option (C): $3
• Time until expiration (T): 60 days

To calculate the potential profit or loss at expiration, you can use the following formula:

Profit/Loss = max(0, S − X) − C

If the stock price (S) at expiration is greater than the strike price (X), the long call is profitable.

Short Call Option

A short call option obligates the seller to sell the underlying stock at the strike price if the option is exercised by the holder. The seller receives a premium for taking on this obligation.

Example:

• Stock DEF’s current price (S): $60
• Strike price (X): $55
• Premium received for the call option (C): $4
• Time until expiration (T): 45 days

To calculate the potential profit or loss at expiration, you can use the following formula:

Profit/Loss = −max(0, S − X) + C

If the stock price (S) at expiration is less than the strike price (X), the short call is profitable.

Long and Short Put Options

Long Put Option

A long put option gives the holder the right to sell the underlying stock at the strike price before or at the expiration date. The holder pays a premium for this right.

Example:

• Stock GHI’s current price (S): $70
• Strike price (X): $65
• Premium paid for the put option (P): $3
• Time until expiration (T): 30 days

To calculate the potential profit or loss at expiration, you can use the following formula:

Profit/Loss = max(0, X − S) − P

If the stock price (S) at expiration is less than the strike price (X), the long put is profitable.

Short Put Option

A short put option obligates the seller to buy the underlying stock at the strike price if the option is exercised by the holder. The seller receives a premium for taking on this obligation.

Example:

• Stock JKL’s current price (S): $45
• Strike price (X): $50
• Premium received for the put option (P): $2
• Time until expiration (T): 20 days

To calculate the potential profit or loss at expiration, you can use the following formula:

Profit/Loss = max(0, X − S) + P

If the stock price (S) at expiration is greater than the strike price (X), the short put is profitable.

Tip: These mathematical examples illustrate the key characteristics and potential outcomes of long and short call and put options. Understanding these concepts is crucial for effective options trading. If you have further questions or would like more information, please feel free to ask.

Strike Price

The strike price (also known as the exercise price) is a critical element in an options contract. It determines the price at which the holder of the option can buy (for call options) or sell (for put options) the underlying asset. Options chains typically list various strike prices, allowing traders to choose the one that aligns with their trading strategy.

Example:

Imagine you’re interested in a call option for stock XYZ:

• Stock XYZ’s current price (S): $60
• Strike price (X): $65
• Premium paid for the call option (C): $3
• Time until expiration (T): 60 days

The strike price (X) in this case is $65. This means that if you exercise the call option, you can buy stock XYZ for $65 per share.

Expiration Date

Every options contract has an expiration date, which is when the option contract becomes void. Options chains typically display options with various expiration dates, ranging from days to years, depending on the stock or index.

Example:

Suppose you’re looking at call options for stock PQR:

• Stock PQR’s current price (S): $75
• Strike price (X): $80
• Premium paid for the call option (C): $4
• Time until expiration (T): 30 days

In this example, the expiration date is 30 days from now. After that date, the option contract will no longer be valid.

Bid and Ask Prices

Options chains display bid and ask prices for each option contract. The bid price is the highest price a buyer is willing to pay for the option, while the ask price is the lowest price a seller is willing to accept. The difference between these two prices is known as the bid-ask spread, and a narrower spread typically indicates higher liquidity.

Example:

For an option on stock LMN:

• Bid price (Bid): $2.50
• Ask price (Ask): $2.60

The bid-ask spread in this case is $0.10, indicating the difference between what buyers are willing to pay and what sellers are asking for.

Volume and Open Interest

Options chains also provide information on volume and open interest. Volume refers to the number of option contracts that have been traded during a specific period, such as a day. Open interest, on the other hand, indicates the total number of contracts that are currently open or held by traders.

Example:

For a put option on stock NOP:

• Volume (Vol): 500 contracts
• Open interest (OI): 1,000 contracts

In this example, 500 contracts were traded during the specified period, while there are a total of 1,000 open contracts.

Implied Volatility

Implied volatility (IV) is a measure of how much the market expects the stock or index’s price to fluctuate. Options chains often display implied volatility values for each option contract. A higher IV typically results in higher option premiums.

Example:

For a call option on stock RST:

• Implied volatility (IV): 0.25 (25%)

In this case, the implied volatility is 25%, suggesting that the market anticipates significant price fluctuations for stock RST.

In-the-Money, At-the-Money, and Out-of-the-Money

Options that are in-the-money (ITM) have intrinsic value, while those that are out-of-the-money (OTM) do not. Options chains often highlight ITM options in a different color or font for easy identification.

Example:

1. Long Call (Buy Call Option):

• Stock: UVW
• Current Stock Price (S): $40
• Strike Price (X): $45

For a long call option, you profit when the stock price (S) rises above the strike price (X).

• If S > X: The call option is in-the-money (profitable).
• If S = X: The call option is at-the-money (no profit or loss).
• If S < X: The call option is out-of-the-money (not profitable).

2. Short Call (Sell Call Option):

• Stock: UVW
• Current Stock Price (S): $40
• Strike Price (X): $45

For a short call, you profit if the stock price stays below the strike price because the option expires worthless.

• If S > X: The short call is out-of-the-money (you face losses since the buyer may exercise).
• If S = X: The short call is at-the-money (no profit or loss yet).
• If S < X: The short call is in-the-money (profitable, as the option likely expires worthless and you keep the premium).

3. Long Put (Buy Put Option):

• Stock: UVW
• Current Stock Price (S): $40
• Strike Price (X): $45

For a long put, you profit when the stock price drops below the strike price.

• If S < X: The put option is in-the-money (profitable).
• If S = X: The put option is at-the-money (no profit or loss).
• If S > X: The put option is out-of-the-money (not profitable).

4. Short Put (Sell Put Option):

• Stock: UVW
• Current Stock Price (S): $40
• Strike Price (X): $45

For a short put, you profit if the stock price stays above the strike price, as the option expires worthless and you keep the premium.

• If S < X: The short put is in-the-money (potential loss as the buyer might exercise).
• If S = X: The short put is at-the-money (no profit or loss yet).
• If S > X: The short put is out-of-the-money (profitable, as the option will likely expire worthless).

Understanding these aspects of options chains is essential for options traders to make informed decisions and develop effective trading strategies. If you have more questions or need further clarification, please feel free to ask.

Options Greeks

Some options chains also display the “Greeks,” which are mathematical measures that describe various risk factors associated with an options position.

The Greeks include:

• Delta
• Gamma
• Theta
• Vega
• Rho

These Greeks help traders understand how the price of an option will change based on factors like the price of the underlying asset, time, and volatility.

Delta

Delta measures how much the price of an option is expected to change for every $1 change in the price of the underlying asset. It indicates the sensitivity of the option’s value to changes in the underlying asset’s price.

Example:

Suppose you hold a call option with a delta of 0.65. If the underlying stock’s price increases by $1, the option’s price is expected to increase by $0.65. Conversely, if the stock price falls by $1, the option’s price should decrease by $0.65.

Gamma

Gamma measures the rate of change of an option’s delta concerning changes in the underlying asset’s price. It quantifies how quickly delta changes as the stock price moves.

Example:

Let’s say you hold a call option with a gamma of 0.03. If the stock price increases by $1, the option’s delta will change by 0.03. In other words, if the delta was initially 0.65, it would become 0.68 after a $1 increase in the stock price.

Theta

Theta measures the rate at which an option’s value declines over time as it approaches its expiration date. It reflects the time decay of options.

Example:

Consider a call option with a theta of -0.04. This means that the option is expected to lose $0.04 in value each day, assuming all other factors remain constant. As you approach the expiration date, theta accelerates the decay in option value.

Vega

Vega measures how sensitive an option’s price is to changes in implied volatility. It quantifies the impact of changes in market expectations of future price volatility.

Example:

Suppose you own a put option with a vega of 0.06. If the implied volatility of the underlying stock increases by 1%, the option’s price is expected to increase by $0.06, all other factors being equal.

Rho

Rho measures how sensitive an option’s price is to changes in interest rates. It quantifies the impact of changes in the risk-free interest rate on the option’s value.

Example:

Let’s say you hold a call option with a rho of 0.02. If the risk-free interest rate increases by 1%, the option’s price is expected to increase by $0.02, assuming all other factors remain constant.

These Greeks help options traders understand and manage the risks associated with their positions. By analyzing these factors, traders can make informed decisions about their options strategies and anticipate how changes in the underlying asset’s price, time, implied volatility, interest rates, and other variables will affect their positions.

Tip: Reading an options chain can seem overwhelming at first, but once you understand its components, it becomes an invaluable tool for making informed trading decisions. By familiarizing yourself with terms like strike price, expiration date, bid-ask spread, and implied volatility, you can better navigate the complex world of options trading.

What Strategies Can You Use for Trading Stock Options?

Stock options offer a wide range of strategies for traders and investors, whether you’re interested in hedging your portfolio, generating income, or speculating on market movements. Below are some of the most commonly used strategies in options trading.

Covered Call

In a covered call strategy, you own the underlying stock and sell call options on that stock to generate income.

Example:

• You own 100 shares of XYZ stock priced at $50 per share.
• You sell one XYZ call option with a strike price of $55 for a premium of $3 per share.

Maximum Profit:

• You receive $300 (100 shares * $3 premium) from selling the call option.
• Your maximum profit is capped at $500 [($55 strike price – $50 purchase price) * 100 shares] plus the $300 premium received.
• Maximum Profit: $800

Maximum Loss:

• If the stock price drops to zero, your loss is $5,000 (100 shares * $50 purchase price).
• However, you keep the $300 premium received.
• Maximum Loss: $4,700

Breakeven Price:

• Your breakeven price is $50 (purchase price of the stock) – $3 (premium received) = $47 per share.

Protective Put

A protective put strategy is used to hedge against potential losses in a stock you own by purchasing a put option.

Example:

• You own 100 shares of ABC stock priced at $60 per share.
• You buy one ABC put option with a strike price of $55 for a premium of $4 per share.

Maximum Profit:

• Unlimited, as you continue to own the stock and benefit from any price increases.

Maximum Loss:

• Your maximum loss is limited to the premium paid for the put option, which is $400 (100 shares * $4 premium).

Breakeven Price:

• There is no specific breakeven point as this strategy is primarily for downside protection.

Bull Call Spread

A bull call spread is a strategy used when you are moderately bullish on a stock. It involves buying a call option at a lower strike price and selling another call option at a higher strike price.

Example:

• You are moderately bullish on XYZ stock, currently trading at $60 per share.
• You buy one XYZ call option with a strike price of $55 for a premium of $4 per share.
• You simultaneously sell one XYZ call option with a strike price of $65 for a premium of $2 per share.

Maximum Profit:

• The maximum profit is the difference between the strike prices ($65 – $55 = $10) minus the net premium paid ($4 – $2 = $2).
• Maximum Profit: $800 (100 shares * $8)

Maximum Loss:

• The maximum loss is the net premium paid, which is $2 per share.
• Maximum Loss: $200 (100 shares * $2)

Breakeven Price:

• Your breakeven price is the strike price of the lower call option plus the net premium paid ($55 + $2 = $57 per share).

Bear Put Spread

A bear put spread is a strategy used when you are moderately bearish on a stock. It involves buying a put option at a higher strike price and selling another put option at a lower strike price.

Example:

• You are moderately bearish on LMN stock, currently trading at $70 per share.
• You buy one LMN put option with a strike price of $75 for a premium of $5 per share.
• You simultaneously sell one LMN put option with a strike price of $65 for a premium of $2 per share.

Maximum Profit:

• The maximum profit is the difference between the strike prices ($75 – $65 = $10) minus the net premium paid ($5 – $2 = $3).
• Maximum Profit: $700 (100 shares * $7)

Maximum Loss:

• The maximum loss is the net premium paid, which is $300.
• Maximum Loss: $300 (100 shares * $3)

Breakeven Price:

• Your breakeven price is the strike price of the higher put option minus the net premium paid ($75 – $3 = $72 per share).

Iron Condor

An iron condor strategy is used when you expect low volatility in the stock price. It involves selling both a call spread and a put spread to take advantage of a narrow trading range.

Example:

• You employ an iron condor strategy on XYZ stock, which is currently trading at $60 per share.
• You sell one out-of-the-money XYZ call option with a strike price of $65 for a premium of $2 per share.
• You sell one out-of-the-money XYZ put option with a strike price of $55 for a premium of $3 per share.
• You simultaneously buy one further out-of-the-money XYZ call option with a strike price of $70 for a premium of $1 per share.
• You simultaneously buy one further out-of-the-money XYZ put option with a strike price of $50 for a premium of $2 per share.

Maximum Profit:

• The maximum profit is the net premium received from selling the call and put options.
• Maximum Profit: $200 ([$2 + $3] – [$1 + $2])

Maximum Loss:

• The maximum loss is the width of the condor ($70 – $50 = $20) minus the net premium received.
• Maximum Loss: $1,800 ([$70 – $50] – [$2 + $3 – $1 – $2])

Breakeven Price:

• The breakeven points occur when the stock price equals the strike price of the short call or short put options plus or minus the net premium received.
• Call side: $65 (short call strike) + $2 (net premium received) = $67 per share
• Put side: $55 (short put strike) – $3 (net premium received) = $52 per share

Long Straddle

A long straddle is a strategy used when you expect significant volatility in the stock’s price but are unsure of the direction. It involves buying both a call option and a put option with the same strike price and expiration date.

Example:

• You implement a straddle strategy on PQR stock, currently trading at $80 per share.
• You buy one PQR call option with a strike price of $80 for a premium of $5 per share.
• You simultaneously buy one PQR put option with a strike price of $80 for a premium of $4 per share.

Maximum Profit:

• Unlimited in either direction, depending on whether the stock price moves significantly up or down.

Maximum Loss:

• The maximum loss is the total premium paid for both the call and put options, which is $9 ($5 + $4) per share.
• Maximum Loss: $900 (100 shares * $9)

Breakeven Price:

• The breakeven points occur when the stock price equals the strike price of the call option plus the total premium paid or equals the strike price of the put option minus the total premium paid.
• Breakeven on the upside: $80 + $9 = $89 per share
• Breakeven on the downside: $80 – $9 = $71 per share

Short Straddle

A short straddle is used when you expect little movement in the stock price. It involves selling both a call option and a put option with the same strike price and expiration date. This strategy profits from low volatility.

Example:

• You sell a short straddle on XYZ stock, currently trading at $70 per share.
• You sell one XYZ call option with a strike price of $70 for a premium of $4 per share.
• You simultaneously sell one XYZ put option with a strike price of $70 for a premium of $3 per share.

Maximum Profit:

• The maximum profit is the total premium received from selling both the call and put options, which is $7 ($4 + $3) per share.
• Maximum Profit: $700 (100 shares * $7)

Maximum Loss:

• The maximum loss is theoretically unlimited if the stock price moves significantly in either direction.
• Maximum Loss: Unlimited on the upside, and substantial on the downside if the stock price drops significantly.

Breakeven Price:

• There is no specific breakeven point for a short straddle as the strategy involves unlimited risk due to significant stock price movements.

Long Strangle

A long strangle is similar to a long straddle, but the options have different strike prices. It is used when you expect significant price movement in the stock but are unsure of the direction.

Example:

• You implement a strangle strategy on UVW stock, currently trading at $90 per share.
• You buy one UVW call option with a strike price of $95 for a premium of $4 per share.
• You simultaneously buy one UVW put option with a strike price of $85 for a premium of $3 per share.

Maximum Profit:

• Unlimited in either direction, depending on whether the stock price moves significantly up or down.

Maximum Loss:

• The maximum loss is the total premium paid for both the call and put options, which is $7 ($4 + $3) per share.
• Maximum Loss: $700 (100 shares * $7)

Breakeven Price:

• The breakeven points occur when the stock price equals the strike price of the call option plus the total premium paid or equals the strike price of the put option minus the total premium paid.
• Breakeven on the upside: $95 + $7 = $102 per share
• Breakeven on the downside: $85 – $7 = $78 per share

Short Strangle

A short strangle is used when you expect little volatility. It involves selling both a call option and a put option with different strike prices. This strategy profits from low volatility but carries unlimited risk if the stock price moves significantly in either direction.

Example:

• You sell a short strangle on LMN stock, currently trading at $85 per share.
• You sell one LMN call option with a strike price of $90 for a premium of $3 per share.
• You simultaneously sell one LMN put option with a strike price of $80 for a premium of $4 per share.

Maximum Profit:

• The maximum profit is the total premium received from selling both the call and put options, which is $7 ($3 + $4) per share.
• Maximum Profit: $700 (100 shares * $7)

Maximum Loss:

• The maximum loss is theoretically unlimited if the stock price moves significantly in either direction.
• Maximum Loss: Unlimited on the upside and substantial if the stock price falls significantly.

Breakeven Price:

• There is no specific breakeven point for a short strangle, as the strategy involves unlimited risk due to significant stock price movements.

These examples illustrate some of the most common options trading strategies, each with its own risk and reward profile. Whether you are using strategies like covered calls, protective puts, or more advanced techniques like straddles and iron condors, the key to success in options trading is understanding the underlying mechanics and how to manage the associated risks.

Tip: Options trading offers a variety of strategies that can be tailored to your market outlook and risk tolerance. Before employing these strategies, it’s crucial to fully understand the potential gains, losses, and risks involved.

Options Trading Strategies for Various Market Outlooks

Options trading offers a plethora of strategies to suit various market outlooks and risk tolerances. Whether you’re new to options or an experienced trader, understanding these strategies can help you make more informed decisions and improve your trading performance. Always remember, options trading involves significant risk, and it’s crucial to understand these strategies thoroughly before implementing them.

How Do You Calculate the Profitability of Stock Options?

Calculating the profitability of stock options is essential for any trader looking to make informed decisions. While options trading can offer high returns, it’s crucial to understand the various factors that contribute to an option’s profitability. Let’s explore how to calculate the profitability of stock options, taking into account premiums, strike prices, and other costs.

Understanding the Basics

Before diving into calculations, it’s important to understand the basic components of an options contract:

• Premium: The price you pay to buy an option or the income you receive when you sell an option.
• Strike Price: The predetermined price at which the option can be exercised.
• Expiration Date: The date when the option contract expires.

Calculating Profit for Option Buyers

For option buyers, the profitability can be calculated using the following formulas:

• Call Option Profit: Max(Stock Price at Expiration – Strike Price, 0) – Premium Paid
• Put Option Profit: Max(Strike Price – Stock Price at Expiration, 0) – Premium Paid

Calculating Profit for Option Sellers

For option sellers, the profitability is the premium received, but you also have to consider the potential losses:

• Call Option Profit: Premium Received – Max(Stock Price at Expiration – Strike Price, 0)
• Put Option Profit: Premium Received – Max(Strike Price – Stock Price at Expiration, 0)

Break-Even Point

The break-even point is the stock price at which an options trade neither makes nor loses money:

• Call Option Break-Even: Strike Price + Premium Paid
• Put Option Break-Even: Strike Price – Premium Paid

Transaction Costs

Don’t forget to factor in transaction costs, such as commissions and fees, which can eat into your profits.

Time Value and Intrinsic Value

Options have both intrinsic value (the in-the-money portion) and time value (the premium above the intrinsic value). Understanding these components can help you assess an option’s profitability potential.

Risk and Reward

While calculating potential profits is important, it’s equally crucial to understand the risks involved. The maximum loss for option buyers is the premium paid, while the maximum loss for option sellers can be much higher.

What is the Role of Market Makers in Options Trading?

In the complex ecosystem of options trading, market makers play a pivotal role in ensuring liquidity and efficient price discovery. Understanding their role can provide traders with valuable insights into how options markets function.

Who Are Market Makers?

Market makers are financial institutions or individuals that are committed to buying and selling options contracts at publicly quoted prices. They facilitate trading by providing liquidity, meaning they stand ready to buy or sell options at any time during market hours.

Providing Liquidity

One of the primary roles of market makers is to provide liquidity to the market. They do this by maintaining a continuous presence, offering to buy and sell options contracts across a range of strike prices and expiration dates.

Price Discovery

Market makers contribute to efficient price discovery by quoting bid and ask prices for options contracts. Their quotes are based on various factors, including the price and volatility of the underlying asset, interest rates, and time to expiration.

Spread and Profit

Market makers profit from the bid-ask spread, which is the difference between the price at which they are willing to buy an option (the bid) and the price at which they are willing to sell it (the ask).

Risk Management

Market makers use sophisticated models to manage the risks associated with holding various options positions.

What Are the Advantages and Disadvantages of Trading Stock Options?

Trading stock options can offer a range of benefits but also comes with its own set of drawbacks. Understanding both the advantages and disadvantages can help traders make more informed decisions.

Advantages

• Leverage: With a small investment, you can control a large amount of stock, potentially amplifying your returns.
• Flexibility: Options offer a high degree of flexibility, allowing you to tailor your positions to your market outlook.
• Risk Management: Options can be used to hedge against potential losses in other investments.
• Income Generation: Strategies like writing covered calls can generate additional income on your existing stock holdings.
• Diversification: Options allow you to gain exposure to various asset classes and market sectors without owning the underlying assets.
• Lower Transaction Costs: In some cases, options can offer a more cost-effective way to gain exposure to a stock.

Disadvantages

• Complexity: Options are complex financial instruments that require a good understanding of the market and the contract terms.
• Risk of Loss: The leverage that amplifies gains can also amplify losses.
• Time Decay: Options lose value over time, which can work against you.
• Liquidity Issues: Not all options are liquid, especially those for less popular stocks or with far-off expiration dates.
• Transaction Costs: Frequent trading can result in significant commissions and fees.
• Tax Implications: Options trading can have complex tax implications, depending on how you use them.

Tip: Trading stock options comes with both advantages and disadvantages. The leverage, flexibility, and risk management benefits can make options a valuable tool for experienced traders. However, the complexity, potential for significant losses, and other drawbacks mean that options are not suitable for everyone. As always, make sure you understand the risks and consult with a financial advisor before diving into options trading.

How Do Stock Options Impact Company Performance?

Stock options are not just tools for traders and investors; they also play a role in corporate governance and employee compensation. The issuance and management of stock options can have a significant impact on a company’s performance.

Employee Incentives

Many companies offer stock options as part of their employee compensation packages. These options give employees the right to buy company stock at a predetermined price, usually after a vesting period. This serves as a powerful incentive for employees to contribute to the company’s success.

Attracting Talent

Offering stock options can make a company more attractive to high-quality talent. This is particularly true for startups and high-growth companies that may not have the cash to offer competitive salaries but can offer the potential for financial gains through stock options.

Dilution of Ownership

Issuing stock options can lead to dilution of ownership for existing shareholders. When options are exercised, new shares are issued, which can reduce the value of existing shares.

Financial Reporting

Stock options can have complex accounting implications. They are often considered a form of non-cash compensation and must be accounted for in the company’s financial statements, affecting metrics like earnings per share (EPS).

Short-Term vs. Long-Term Focus

One criticism of stock options is that they can encourage a short-term focus among employees and executives. If options are set to expire soon, there may be a temptation to take actions that boost the stock price in the short term, potentially at the expense of long-term success.

Tax Implications

Both the company and employees face tax considerations when dealing with stock options. Companies may receive tax benefits from the issuance of options, while employees may face complex tax situations when exercising them.

Market Perception

The way a company manages its stock options can influence its perception by investors. Transparent and responsible management of stock options can boost investor confidence, while poor management or overly generous option grants can raise red flags.

What Are the Differences Between American and European Stock Options?

When it comes to trading stock options, it’s crucial to understand the different types available. Two of the most common are American and European options, which share similarities but have key differences.

Exercise Timing

• American Options: Can be exercised at any time before the expiration date.
• European Options: Can only be exercised at the expiration date.

American Option Example

Imagine you hold an American call option on Company XYZ. This option grants you the right to buy one share of XYZ stock at a strike price of $50. The current stock price is $55, and the option expires in one month.

American Call Option Payoff at Expiration

• If the stock price at expiration is $60, you would exercise the option to buy the stock at the strike price of $50 and then sell it at the market price of $60.
• Your profit per share would be calculated as $60 (selling price) – $50 (strike price) = $10 profit.

American Call Option Payoff Before Expiration (0.5 months before expiration)

• Let’s say the stock price rises to $58, and there is still half a month until expiration.
• You could choose to exercise the option early, buying the stock at the strike price of $50 and selling it at the current market price of $58.
• Your profit per share would be $58 (selling price) – $50 (strike price) = $8 profit.

Tip: American call options provide the flexibility to exercise at any time before expiration, which can be advantageous in volatile markets.

European Option Example

Now, imagine you hold a European put option on Company ABC. This option allows you to sell one share of ABC stock at a strike price of $70. The current stock price is $65, and the option also expires in one month.

European Put Option Payoff at Expiration

• If the stock price at expiration is $60, you would exercise the option to sell the stock at the higher strike price of $70, despite the lower market price.
• Your profit per share would be $70 (strike price) – $60 (selling price) = $10 profit.

European Put Option Payoff Before Expiration (0.5 months before expiration)

• If the stock price falls to $62 with 0.5 months remaining until expiration, you cannot exercise the option early.
• However, if the stock price remains at $62 until expiration, you can exercise the option at that time to sell the stock at the strike price of $70.
• Your profit per share would be $70 (strike price) – $62 (selling price) = $8 profit.

Tip: European put options can only be exercised on the expiration date, which means they don’t offer the flexibility of American options to be exercised early.

Flexibility

American options offer greater flexibility as they can be exercised at any time. This can be advantageous in scenarios where you want to capture dividends or react to significant news affecting the underlying stock.

Option Pricing

American options are generally more expensive than European options due to the added flexibility. However, the price difference is often minimal for options on non-dividend-paying stocks.

Dividends

If the underlying stock pays dividends, American call options are more valuable because they allow the holder to exercise before a dividend payment.

Risk for Sellers

American options pose a higher risk for option sellers due to the potential for early assignment, whereas European options can only be exercised at expiration.

Availability

In the U.S., most exchange-traded stock options are American-style, while index options are often European-style. In European markets, European-style options are more common.

Tax Implications

The different exercise rules can lead to different tax implications. American options may trigger tax events if exercised early, while European options offer more predictability.

Settlement

European options often use cash settlement, meaning that no actual shares are exchanged when the option is exercised. American options usually involve the transfer of the underlying asset, although cash-settled American options do exist.

Tip: Understanding the differences between American and European stock options is crucial for any trader. The primary distinction lies in the exercise timing, but other factors like pricing, risk for sellers, and tax implications also play a role. By knowing these differences, you can choose the option type that best suits your trading strategy and risk tolerance.

What is Options Moneyness and How Does It Affect Trading?

In options trading, “moneyness” describes the relationship between the option’s strike price and the current price of the underlying asset. Understanding moneyness is crucial as it affects not only the option’s price but also the trading strategies you might employ.

Types of Moneyness

• In-the-Money (ITM): For call options, this means the stock price is above the strike price. For put options, the stock price is below the strike price.
• At-the-Money (ATM): The stock price is equal to or very close to the strike price.
• Out-of-the-Money (OTM): For call options, the stock price is below the strike price. For put options, the stock price is above the strike price.

Long Call Option Examples

Scenario 1: In-The-Money (ITM) Long Call Option

• Stock Price (S): $60
• Strike Price (K): $55
• Premium (C): $8

Payoff at Expiration (T):

• If the stock price (S) is greater than the strike price (K), you profit. In this case, the option is ITM.
• Payoff = Max(S – K, 0) – Premium
• Payoff = Max($60 – $55, 0) – $8 = $2 profit.

Scenario 2: At-The-Money (ATM) Long Call Option

• Stock Price (S): $55
• Strike Price (K): $55
• Premium (C): $6

Payoff at Expiration (T):

• If the stock price (S) is equal to the strike price (K), the option is ATM.
• Payoff = Max(S – K, 0) – Premium
• Payoff = Max($55 – $55, 0) – $6 = $0 (break-even).

Scenario 3: Out-Of-The-Money (OTM) Long Call Option

• Stock Price (S): $50
• Strike Price (K): $55
• Premium (C): $4

Payoff at Expiration (T):

• If the stock price (S) is less than the strike price (K), the option is OTM, and you incur a loss.
• Payoff = Max(S – K, 0) – Premium
• Payoff = Max($50 – $55, 0) – $4 = -$4 loss.

Short Call Option Examples

Scenario 1: In-The-Money (ITM) Short Call Option

• Stock Price (S): $60
• Strike Price (K): $55
• Premium (C): $8

Payoff at Expiration (T):

• If the stock price (S) is greater than the strike price (K), you incur a loss. In this case, the option is ITM.
• Payoff = -(Max(S – K, 0) – Premium)
• Payoff = -[Max($60 – $55, 0) – $8] = -$2 loss.

Scenario 2: At-The-Money (ATM) Short Call Option

• Stock Price (S): $55
• Strike Price (K): $55
• Premium (C): $6

Payoff at Expiration (T):

• If the stock price (S) is equal to the strike price (K), the option is ATM.
• Payoff = -(Max(S – K, 0) – Premium)
• Payoff = -[Max($55 – $55, 0) – $6] = $6 gain.

Scenario 3: Out-Of-The-Money (OTM) Short Call Option

• Stock Price (S): $50
• Strike Price (K): $55
• Premium (C): $4

Payoff at Expiration (T):

• If the stock price (S) is less than the strike price (K), you do not incur a loss. In this case, the option is OTM.
• Payoff = -(Max(S – K, 0) – Premium)
• Payoff = -[Max($50 – $55, 0) – $4] = $4 gain.

Long Put Option Examples

Scenario 1: In-The-Money (ITM) Long Put Option

• Stock Price (S): $45
• Strike Price (K): $50
• Premium (P): $7

Payoff at Expiration (T):

• If the stock price (S) is less than the strike price (K), the option is ITM, and you profit.
• Payoff = Max(K – S, 0) – Premium
• Payoff = Max($50 – $45, 0) – $7 = $3 profit.

Scenario 2: At-The-Money (ATM) Long Put Option

• Stock Price (S): $50
• Strike Price (K): $50
• Premium (P): $6

Payoff at Expiration (T):

• If the stock price (S) is equal to the strike price (K), the option is ATM.
• Payoff = Max(K – S, 0) – Premium
• Payoff = Max($50 – $50, 0) – $6 = $0 (break-even).

Scenario 3: Out-Of-The-Money (OTM) Long Put Option

• Stock Price (S): $55
• Strike Price (K): $50
• Premium (P): $4

Payoff at Expiration (T):

• If the stock price (S) is greater than the strike price (K), the option is OTM, and you incur a loss.
• Payoff = Max(K – S, 0) – Premium
• Payoff = Max($50 – $55, 0) – $4 = -$4 loss.

Short Put Option Examples

Scenario 1: In-The-Money (ITM) Short Put Option

• Stock Price (S): $45
• Strike Price (K): $50
• Premium (P): $7

Payoff at Expiration (T):

• If the stock price (S) is less than the strike price (K), you incur a loss. In this case, the option is ITM.
• Payoff = -(Max(K – S, 0) – Premium)
• Payoff = -[Max($50 – $45, 0) – $7] = -$3 loss.

Scenario 2: At-The-Money (ATM) Short Put Option

• Stock Price (S): $50
• Strike Price (K): $50
• Premium (P): $6

Payoff at Expiration (T):

• If the stock price (S) is equal to the strike price (K), the option is ATM.
• Payoff = -(Max(K – S, 0) – Premium)
• Payoff = -[Max($50 – $50, 0) – $6] = -$6 loss.

Scenario 3: Out-Of-The-Money (OTM) Short Put Option

• Stock Price (S): $55
• Strike Price (K): $50
• Premium (P): $4

Payoff at Expiration (T):

• If the stock price (S) is greater than the strike price (K), you do not incur a loss. In this case, the option is OTM.
• Payoff = -(Max(K – S, 0) – Premium)
• Payoff = -[Max($50 – $55, 0) – $4] = $4 gain.

Impact on Premium

• ITM Options: Have intrinsic value and are generally more expensive.
• ATM Options: Have no intrinsic value but have time value, making them moderately priced.
• OTM Options: Have neither intrinsic nor time value and are generally the cheapest.

Trading Strategies Based on Moneyness

• ITM Options: Suitable for conservative strategies like covered calls or protective puts.
• ATM Options: Useful for strategies that benefit from price movements, such as long or short straddles.
• OTM Options: Often used in speculative strategies aiming for high returns but with higher risk.

Time Decay

• ITM Options: Less affected by time decay.
• ATM and OTM Options: More susceptible to time decay, especially as expiration approaches.

Liquidity

• ITM and ATM Options: Typically have higher liquidity.
• OTM Options: May have lower liquidity, leading to wider bid-ask spreads.

Risk and Reward

• ITM Options: Lower risk but also lower potential returns.
• OTM Options: Higher risk but also the potential for higher returns.

Tip: Understanding Options Moneyness and grasping the concept of options moneyness is essential for any trader. It affects various aspects of trading, including the option’s price, the suitability for different strategies, and the risk-reward profile. By understanding how moneyness impacts your trades, you can make more informed decisions and develop strategies that align with your trading goals and risk tolerance.

How Do Market Conditions Affect Options Pricing?

Options pricing is influenced by several key factors, such as the price of the underlying asset, time until expiration, and volatility. However, broader market conditions can also significantly impact options pricing. Let’s explore how various market conditions affect the cost of options.

Volatility

Market volatility plays a critical role in determining options prices. When markets are volatile, the potential for large price swings in the underlying asset increases, making options more expensive.

• High Volatility: Leads to higher premiums for both call and put options.
• Low Volatility: Results in lower premiums.

Interest Rates

Changes in interest rates can also impact options pricing, though their influence is typically smaller than other factors.

• Rising Interest Rates: Tend to increase call option prices and decrease put option prices.
• Falling Interest Rates: Have the opposite effect, lowering call option prices and raising put option prices.

Market Sentiment

The general mood of the market can influence the demand for call or put options. In bullish markets, call options might experience higher demand, raising premiums, while in bearish markets, put options tend to become more expensive.

Dividends

Dividends paid by the underlying asset can affect options pricing.

• Upcoming Dividends: Can increase the price of put options and decrease the price of call options.

Liquidity

The ability to easily buy or sell options affects their price.

• High Liquidity: Narrows bid-ask spreads, making trades easier and more cost-effective.
• Low Liquidity: Widens bid-ask spreads, which may impact profitability.

Economic Indicators

Major economic announcements, such as employment reports or GDP data, can increase market volatility, which in turn can affect options pricing.

Geopolitical Events

Uncertainty caused by geopolitical events—such as elections, trade wars, or conflicts—often leads to higher volatility, raising options premiums.

Supply and Demand

As with any financial asset, supply and demand affect options prices. High demand for specific options can drive up their prices regardless of other market conditions.

Tip: Understanding how market conditions influence options pricing is essential for traders to make informed decisions. Factors like volatility, interest rates, and market sentiment all play a role in determining the cost of entering and exiting options trades. By monitoring these factors, traders can better navigate the market and optimize their strategies.

How is the Black-Scholes Model Used in Options Pricing?

The Black-Scholes model is one of the most widely used methods for pricing European-style options. Developed by economists Fischer Black, Myron Scholes, and Robert Merton, it provides a theoretical estimate for the price of these options. Let’s take a closer look at how the Black-Scholes model is applied to options pricing.

The Black-Scholes Formula

The Black-Scholes formula for calculating the price of a European call option is:

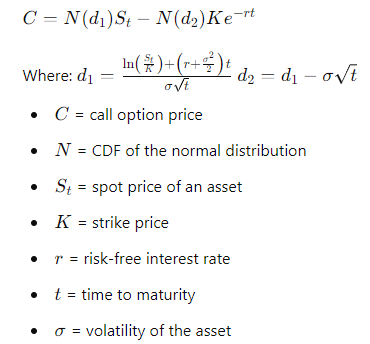
Example Calculation Let’s say we have a European call option with the following parameters:

• S = $50
• X = $45
• T = 1 year
• r = 0.05 or 5%
• σ = 0.2 or 20%

First, we calculate d1 and d2:

Next, we find N(d1) and N(d2). Using standard normal distribution tables or a calculator, we get:

• N(d1) = 0.7291
• N(d2) = 0.6591

Finally, we plug these into the Black-Scholes formula:

Limitations While the Black-Scholes model is incredibly useful, it has its limitations. It assumes constant volatility and interest rates, and it does not account for dividends. Modifications and extensions have been developed to address these limitations.

Tip: The Black-Scholes model provides a theoretical framework for pricing European options, offering traders a mathematical approach to make informed decisions.

While it has its limitations, understanding the Black-Scholes model can give you a significant edge in the complex world of options trading.

What is the Concept of Delta in Options Trading? In options trading, Delta is one of the “Greeks” that helps traders understand the risk and potential reward of an options position. Specifically, Delta measures how much an option’s price is expected to change for a $1 change in the underlying asset.

In this article, we’ll explore the concept of Delta in options trading and illustrate its application with mathematical examples.

Understanding Delta Delta is expressed as a number between -1 and 1. For call options, Delta ranges from 0 to 1, while for put options, it ranges from -1 to 0.

• Call Option Delta: If a call option has a Delta of 0.6, the option’s price is expected to increase by $0.60 for every $1 increase in the underlying stock.
• Put Option Delta: If a put option has a Delta of -0.4, the option’s price is expected to increase by $0.40 (or decrease by -$0.40) for every $1 increase in the underlying stock.

Delta and Position Sizing Delta can also be used to understand the equivalent exposure of an options position to the underlying asset. For example, if you own 100 call options with a Delta of 0.6, your position is equivalent to owning 100×0.6×100=6000 shares of the stock.

Example Calculation Let’s say you have a call option with a Delta of 0.5 and the stock price increases by $2. The expected change in the option price would be:
Delta × Change in Stock Price = 0.5 × 2 = $1
If the option was initially priced at $3, the new price would be 3 + 1 = $4.

Delta Hedging Delta hedging involves taking positions in the underlying asset to offset the Delta of your options position. For example, if you own 100 call options with a Delta of 0.6, you could short 100×0.6×100=6000 shares to create a Delta-neutral position.

Factors Affecting Delta Delta is not constant; it changes with the stock price, time to expiration, and volatility. For instance, an at-the-money (ATM) option will have a Delta close to 0.5, but this will change as the stock price moves.

Tip: Understanding Delta is crucial for any options trader as it provides insights into the risk and potential reward of an options position. It can be used for position sizing, risk management, and even crafting complex trading strategies like Delta hedging. By incorporating Delta into your trading toolkit, you can make more informed decisions and better manage your options portfolio.

What is Implied Volatility in Options Trading? Implied Volatility (IV) is a crucial concept in options trading that reflects the market’s expectation of future volatility in the price of the underlying asset.

It is derived from the current price of an option and represents the market’s forecast of how much the underlying asset is likely to fluctuate. In this article, we’ll delve into the concept of Implied Volatility and illustrate its importance with mathematical examples.

Understanding Implied Volatility Implied Volatility is expressed as an annualized percentage and is a key component in options pricing models like the Black-Scholes model.

A higher IV indicates that the market expects significant price swings, making the option more expensive. Conversely, a lower IV suggests that the market expects less volatility, resulting in cheaper options.

Calculating Implied Volatility Implied Volatility is generally calculated using iterative methods like the Newton-Raphson method to solve the Black-Scholes formula for σ (volatility). Given that the Black-Scholes formula for a European call option is:

The goal is to find the σ that makes the theoretical price C equal to the market price of the option.

Example Calculation Let’s say we have a European call option with a market price of $9, and the following parameters:

• S = $50
• X = $45
• T = 1 year
• r = 0.05 or 5%

Using an iterative method, we find that the Implied Volatility σ that makes the theoretical price equal to $9 is approximately 0.22 or 22%.

Implied Volatility and Trading Strategies Different levels of IV are suitable for different trading strategies:

• High IV: Good for selling options strategies like covered calls or iron condors.
• Low IV: Suitable for buying options strategies like long calls or straddles.

Implied Volatility Skew

Implied Volatility Skew Sometimes, the IV varies for options with different strike prices or expiration dates. This phenomenon is known as the “volatility skew.” For example, if out-of-the-money puts have a higher IV than at-the-money options, it indicates that the market expects a potential downside move.

Tip: Understanding Implied Volatility is essential for any options trader. It not only affects the price of options but also provides insights into market sentiment and potential future volatility. By incorporating IV into your trading decisions, you can better assess the risk and potential reward, allowing for more informed and strategic trading.

What is the Time Value of an Option?

In options trading, the price of an option is composed of intrinsic value and time value. While intrinsic value is straightforward, representing the immediate profitability of an option, time value is a bit more complex. It accounts for the potential future profitability of the option. In this article, we’ll explore the concept of the time value of an option and illustrate its application with mathematical examples.

Understanding Time Value

The time value of an option is the portion of the option’s premium that exceeds its intrinsic value. Mathematically, it can be expressed as:

Time Value = Option Premium − Intrinsic Value

Factors Affecting Time Value

• Time value is influenced by several factors, including:
• Time until expiration: More time allows for greater price movement in the underlying asset.
• Volatility: Higher volatility increases the chance of the option becoming profitable.
• Interest rates: Higher interest rates can slightly increase the time value.

Example Calculation

Let’s say you have a call option for stock XYZ with the following parameters:

• Current stock price (S) = $50
• Strike price (X) = $45
• Option premium = $8

First, we calculate the intrinsic value:

Intrinsic Value = S – X = $50 – $45 = $5

Next, we find the time value:

Time Value = Option Premium – Intrinsic Value = $8 – $5 = $3

Time Decay

As the option approaches its expiration date, the time value decreases, a phenomenon known as “time decay.” The rate of time decay is quantified by another Greek, Theta, which indicates how much an option’s price will decrease for a one-day change in time.

For example, if an option has a Theta of -0.05, the option’s price will decrease by $0.05 per day due to time decay alone.

Time Value and Trading Strategies

Understanding time value is crucial for various trading strategies:

Buying Options: Look for options with high time value if you expect significant price movement before expiration.

Selling Options: Opt for options with low time value to take advantage of time decay.

Tip: The time value of an option is a critical concept that every options trader should understand. It represents the market’s expectation of the option’s future profitability and is influenced by various factors like time until expiration, volatility, and interest rates. By understanding time value and how it decays, traders can make more informed decisions and select strategies that align with their market outlook and risk tolerance.

What is the Concept of Gamma in Options Trading?

Gamma is another member of the “Greeks” family in options trading, and it measures how much an option’s Delta is expected to change for a $1 change in the underlying asset. In other words, Gamma gives you a sense of the acceleration of an option’s price change. In this article, we’ll explore the concept of Gamma in options trading and illustrate its application with mathematical examples.

Understanding Gamma

Gamma is expressed as a positive number and applies to both call and put options. A higher Gamma means that the option’s Delta will change more rapidly with changes in the underlying asset’s price.

• High Gamma: Indicates that the option’s Delta will change significantly even for small changes in the stock price.
• Low Gamma: Suggests that the option’s Delta will change minimally for small changes in the stock price.

Gamma and Delta Relationship

Mathematically, Gamma (Γ) is the derivative of Delta with respect to the stock price, and it can be expressed as:

Example Calculation

Let’s say you have a call option with a Delta of 0.5 and a Gamma of 0.1. If the stock price increases by $2, the new Delta would be calculated as follows:

New Delta = Old Delta + (Γ × Change in Stock Price)

New Delta = 0.5 + (0.1 × 2) = 0.5 + 0.2 = 0.7

Gamma and Trading Strategies

Understanding Gamma is crucial for various trading strategies:

• Long Options: High Gamma is generally favorable because it amplifies the effect of price movements in the underlying asset.
• Short Options: Low Gamma is preferable to minimize the risk associated with rapid changes in Delta.

Gamma Hedging

Gamma hedging involves taking positions to offset the Gamma of your options portfolio, aiming to make it Gamma-neutral. This is often done by buying and selling options with different Gammas.

Gamma and Time Decay

As the option approaches expiration, Gamma tends to increase for at-the-money options, making them more sensitive to changes in the underlying asset’s price. This is important for traders to consider, especially when holding options close to expiration.

Tip: Gamma is an essential concept in options trading that helps traders understand the rate of change of an option’s Delta. It provides insights into the sensitivity of an option’s price to changes in the underlying asset and is crucial for risk management and strategy selection. By understanding Gamma and its implications, traders can make more informed decisions and better manage their options portfolio.

What is the Concept of Vega in Options Trading?

Vega is another important “Greek” in the realm of options trading. It measures the sensitivity of an option’s price to changes in the volatility of the underlying asset. In this article, we’ll explore the concept of Vega in options trading and illustrate its application with mathematical examples.

Understanding Vega

Vega is expressed as the amount an option’s price will change for a 1% change in implied volatility. Unlike Delta and Gamma, Vega is not restricted by a range and can be any positive number.

• High Vega: Indicates that the option’s price will change significantly for a small change in implied volatility.
• Low Vega: Suggests that the option’s price will change minimally for a small change in implied volatility.

Vega and Option Pricing

Mathematically, Vega (ν) can be expressed as the partial derivative of the option price with respect to the volatility (σ):

Example Calculation

Let’s say you have a call option with a premium of $5 and a Vega of 0.2. If the implied volatility increases by 2%, the new premium would be calculated as follows:

New Premium = Old Premium+(Vega * Change in Implied Volatility)

New Premium = $5 + (0.2 times 2) = $5 + 0.4 = $5.4

Vega and Trading Strategies Understanding Vega is crucial for various trading strategies:

• Long Volatility: If you expect volatility to increase, look for options with high Vega.
• Short Volatility: If you expect volatility to decrease, look for options with low Vega or consider selling options.

Vega and Time to Expiration Vega generally increases as the time to expiration increases, making long-term options more sensitive to changes in implied volatility.

Vega Hedging

Vega hedging involves taking positions to offset the Vega of your options portfolio, aiming to make it Vega-neutral. This is often done by buying and selling options with different Vegas.

Tip: Vega is an essential concept in options trading that helps traders understand the sensitivity of an option’s price to changes in volatility. It provides insights into how changes in market conditions can affect an option’s price and is crucial for risk management and strategy selection. By understanding Vega and its implications, traders can make more informed decisions and better manage their options portfolio.

The Concept of Rho in Options Trading

Rho is one of the lesser-known “Greeks” in options trading, but it’s still important for a comprehensive understanding of risk and strategy.

Rho measures the sensitivity of an option’s price to changes in interest rates. In this article, we’ll explore the concept of Rho in options trading and illustrate its application with mathematical examples.

Understanding Rho Rho is expressed as the amount an option’s price will change for a 1% change in interest rates. It is usually a smaller number compared to other Greeks like Delta and Gamma.

• Positive Rho: Indicates that the option’s price will increase if interest rates rise.
• Negative Rho: Suggests that the option’s price will decrease if interest rates rise.

Rho and Option Pricing Mathematically, Rho (ρ) can be expressed as the partial derivative of the option price with respect to the interest rate (r):

Example Calculation

Let’s say you have a call option with a premium of $10 and a Rho of 0.05. If interest rates increase by 1%, the new premium would be calculated as follows:

New Premium = Old Premium + (Rho * Change in Interest Rates)
New Premium = $10 + (0.05 × 1) = $10 + 0.05 = $10.05

Rho and Trading Strategies Understanding Rho is crucial for various trading strategies:

• Long Calls/Puts: If you’re buying options and expect interest rates to rise, consider options with a positive Rho.
• Short Calls/Puts: If you’re selling options and expect interest rates to fall, look for options with a negative Rho.

Rho and Time to Expiration

Rho generally increases as the time to expiration increases, making long-term options more sensitive to changes in interest rates.

Tip: While Rho may not be as widely discussed as other Greeks like Delta or Vega, it’s still an important factor to consider, especially in an environment where interest rates are volatile. Rho gives you an idea of how sensitive your options portfolio is to changes in interest rates, allowing for more informed decision-making and risk management.

What are Synthetic Options in Options Trading?

Synthetic options refer to options positions that mimic the payoff of other financial instruments using a combination of options and the underlying asset. These synthetic structures are used to replicate the behavior of other options or even stocks or etf’s. In this article, we’ll delve into the concept of synthetic options and illustrate their application with mathematical examples.

Understanding Synthetic Options A synthetic option is created by combining long or short positions in the underlying asset with long or short positions in options. The most common synthetic options include:

• Synthetic Long Stock: Created by buying a call option and selling a put option with the same strike price and expiration date.
• Synthetic Short Stock: Created by selling a call option and buying a put option with the same strike price and expiration date.

Mathematical Representation The payoff of a synthetic long stock can be represented as:
Payoff = C − P + S
Where C is the payoff from the long call, P is the payoff from the short put, and S is the stock price at expiration.

Example Calculation Let’s say you create a synthetic long stock by buying a call option with a premium of $2 and selling a put option with a premium of $1. The stock price at expiration is $50. The payoff would be:

Payoff = (50 − 2) − (50 − 1) + 50 = 48 − 49 + 50 = 49

This payoff mimics owning the stock outright, which would also result in a $49 payoff if purchased at $50 and sold at $49.

Synthetic Options and Trading Strategies Synthetic options are useful for various trading strategies:

• Risk Management: They can be used to hedge existing positions.
• Cost Efficiency: Sometimes, creating a synthetic position is cheaper than buying the actual financial instrument.
• Flexibility: They offer more strategic options for traders who want to express a particular market view.

Tip: While synthetic options may seem complex, they offer traders a way to mimic the behavior of other financial instruments without actually owning them. Understanding how to create and use synthetic options can provide you with additional tools for risk management, cost efficiency, and strategic flexibility. By incorporating synthetic options into your trading toolkit, you can make more informed decisions and better manage your options portfolio.

What is the Concept of Leverage in Options Trading?

Leverage is a double-edged sword in the world of options trading. It allows traders to control a large position with a relatively small amount of capital. While this can amplify profits, it can also magnify losses. In this article, we’ll explore the concept of leverage in options trading and illustrate its application with mathematical examples.

Understanding Leverage In options trading, leverage is the ability to control a large position in an underlying asset with a relatively small investment. The leverage factor is often calculated as:

Example Calculation

Let’s say you buy a call option for stock XYZ with a strike price of $50 and a premium of $5. The leverage factor would be:

Leverage Factor = 50 / 5 = 10

This means you are controlling $50 worth of the stock with just $5, effectively leveraging your position by a factor of 10.

Leverage and Risk While leverage can amplify returns, it also increases risk. For example, if the stock price falls to $45, the option could become worthless, resulting in a 100% loss, whereas owning the stock outright would result in only a 10% loss.

Leverage and Trading Strategies

Different options strategies have different leverage profiles:

• Covered Calls: Low leverage, as you own the underlying stock.
• Naked Puts: High leverage, as you’re obligated to buy the stock but don’t own it.
• Spreads: Variable leverage, depending on the strike prices and premiums of the options involved.

Tip: Leverage in options trading is a powerful tool that can both amplify gains and magnify losses. Understanding how leverage works and how it fits into your overall trading strategy is crucial for managing risk and maximizing returns. By incorporating the concept of leverage into your trading toolkit, you can make more informed decisions and better manage your options portfolio.

How to Calculate the Probability of Profit in Options Trading

Calculating the probability of profit is a vital aspect of options trading, as it helps traders assess the likelihood of a successful trade. In this article, we’ll explore how to calculate the probability of profit in options trading and provide mathematical examples to illustrate the process.

The Probability of Profit Formula The probability of profit can be calculated using mathematical models, with one of the most common being the Black-Scholes model. In this model, the formula for calculating the probability of profit for a long call option is as follows:

Probability of Profit = N(d2)

Where:

In this formula:

• S is the current stock price.
• X is the strike price of the option.
• T is the time until expiration in years.
• r is the risk-free interest rate.
• σ is the volatility of the stock.

Example Calculation

Let’s say you are considering a long call option with the following parameters:

• Current stock price (S): $50
• Strike price (X): $55
• Time until expiration (T): 0.5 years
• Risk-free interest rate (r): 0.05 (5%)
• Volatility (σ): 0.2 (20%)

Using the Black-Scholes model, you would calculate d2 as follows:

Solving for d2, you would find the value. Finally, you would use the cumulative distribution function to find the probability of profit, which corresponds to N(d2).

Tip: Calculating the probability of profit is a valuable tool for options traders, as it provides insights into the likelihood of a successful trade. By understanding the mathematical models and parameters involved, traders can make more informed decisions and better manage their options portfolios.

The Importance of Risk Management in Options Trading Risk management is a cornerstone of successful options trading. It involves strategies and techniques to minimize potential losses and protect your capital. In this article, we’ll explore the importance of risk management in options trading and provide mathematical examples to illustrate key concepts.

The Risk-Reward Tradeoff

Options trading offers the potential for significant returns, but it also carries inherent risks. The risk-reward tradeoff is a fundamental concept. Traders must balance the potential for profit with the risk of losses.

Position Sizing

One key aspect of risk management is position sizing. This involves determining the appropriate size of your options positions relative to your overall capital. Position sizing helps limit the impact of individual trades on your portfolio.

Example: Position Sizing

Let’s say you have a $100,000 trading account, and you’re willing to risk 2% of your capital on a single trade. If you’re considering an options trade with a potential loss of $2,000, you would calculate your position size as:

This means you would limit your position to one contract to adhere to your risk management rules.

Diversification

Another crucial risk management technique is diversification. Diversifying your options positions across different underlying assets or strategies can help spread risk.

Example: Diversification

Suppose you have a $100,000 portfolio, and you want to diversify across different stocks. You allocate $20,000 to each of five different stocks, and you trade options on each of them. If one stock experiences a significant adverse move, the impact on your overall portfolio is limited.

Tip: Risk management is the cornerstone of successful options trading. By understanding position sizing, diversification, and other risk management techniques, traders can protect their capital and trade with confidence. Remember that risk management is a personalized process, and it’s essential to tailor it to your risk tolerance and trading strategy.

The Role of the Option Delta in Portfolio Hedging

The Delta of an option measures the sensitivity of its price to changes in the price of the underlying asset. It plays a crucial role in managing risk and hedging in options trading. In this article, we’ll explore how the option Delta can be used for portfolio hedging and provide mathematical examples to illustrate its application.

The Concept of Delta

Delta is one of the Greeks used to quantify an option’s risk exposure to changes in the underlying asset’s price. It ranges from -1 to 1 for put options and 0 to 1 for call options. A Delta of 0.5 for a call option means that for every $1 increase in the underlying asset’s price, the option’s price will increase by $0.50.

Portfolio Hedging with Delta

Delta can be used to hedge a portfolio of options and underlying assets. By creating an offsetting Delta position, traders can protect their portfolio from adverse price movements.

Mathematical Example

Suppose you have a portfolio of call options with a total Delta of 0.8 and an underlying asset with a Delta of -0.6. To hedge your portfolio against potential losses, you would calculate the net Delta:

Net Delta = Portfolio Delta + Underlying Asset Delta

Net Delta = 0.8−0.6 = 0.2

A net Delta of 0.2 indicates that for every $1 move in the underlying asset’s price, your portfolio will gain or lose $0.20, effectively hedging against a portion of the risk.

Tip: The option Delta is a valuable tool for portfolio hedging in options trading. By understanding the Delta of your options and underlying assets, you can create strategies to mitigate risk and protect your investments. Keep in mind that Delta is just one of several factors to consider when managing a portfolio, and it should be used in conjunction with other risk management techniques.

Understanding the Put-Call Parity in Options Trading

The put-call parity is a fundamental concept in options trading that relates the prices of European call and put options with the same strike price and expiration date. It provides a powerful tool for arbitrage and understanding the relationship between these options. In this article, we’ll explore the put-call parity and provide mathematical examples to illustrate its application.

The Put-Call Parity Equation

Where:

• C = Price of the European call option
• P = Price of the European put option
• S = Current price of the underlying asset
• X = Strike price of the options
• r = Risk-free interest rate
• T = Time until expiration

Example Calculation

Suppose you have the following information:

• Time until expiration (T): 1 yeare put-call parity equation is as follows:
• European call option price (C): $8
• European put option price (P): $6
• Current price of the underlying asset (S): $50
• Strike price of the options (X): $45
• Risk-free interest rate (r): 0.05 (5%)

You can calculate r from the equation.

Tip: Understanding the put-call parity is essential for options traders as it helps identify mispriced options and arbitrage opportunities. By utilizing this relationship, traders can make more informed decisions and potentially profit from market inefficiencies. Remember that put-call parity holds for European options, so it may not apply to American-style options.

The Role of Implied Volatility in Options Pricing

Implied volatility is a critical factor in options pricing. It represents the market’s expectation of future price fluctuations and plays a significant role in determining an option’s premium. In this article, we’ll explore the role of implied volatility in options pricing and provide mathematical examples to illustrate its impact.

Understanding Implied Volatility

Implied volatility is a measure of the expected future volatility of the underlying asset’s price. It is often derived from the option’s market price using mathematical models like the Black-Scholes model.

The Impact of Implied Volatility on Options Pricing

Implied volatility has a direct impact on an option’s premium. Generally, higher implied volatility leads to higher option premiums, while lower implied volatility results in lower premiums.

Example Calculation

Let’s 

• Current stock price (S): $50
• Strike price (X): $55
• Time until expiration (T): 0.5 years
• Risk-free interest rate (r): 0.05 (5%)

Suppose you have two scenarios with different implied volatilities:

Scenario 1: Implied Volatility (σ) = 0.2 (20%) Scenario 2: Implied Volatility (σ) = 0.3 (30%)

You can use the Black-Scholes model to calculate the option premium (C) for both scenarios:

Where d1 and d2 are calculated using the given parameters and implied volatilities for each scenario.

Compare the option premiums in both scenarios to see the impact of implied volatility on options pricing.

Tip: Implied volatility is a key driver of options pricing, and understanding its impact is crucial for options traders. Higher implied volatility indicates greater expected price fluctuations and leads to higher option premiums. Conversely, lower implied volatility results in lower premiums. Traders should assess implied volatility when selecting options strategies and managing their portfolios to make more informed decisions.

The Role of Theta in Options Decay

Theta, often referred to as ”time decay,” is a critical factor in options pricing. It measures the rate at which an option’s premium erodes as time passes, and it plays a significant role in options trading strategies. In this article, we’ll explore the role of Theta in options decay and provide mathematical examples to illustrate its impact.

Understanding Theta

Theta represents the time decay of an option’s premium. It quantifies how much an option’s value decreases with each day that passes, assuming all other factors remain constant. Theta is typically expressed as a negative value because it reflects the diminishing value of the option over time.

Theta and Options Pricing

Theta’s impact on options pricing becomes more pronounced as an option approaches its expiration date. At that point, Theta accelerates the premium’s decay.

Example Calculation

Let’s consider a call option for stock ABC with the following parameters:

• Current stock price (S): $50
• Strike price (X): $55
• Time until expiration (T): 30 days
• Risk-free interest rate (r): 0.05 (5%)
• Volatility (σ): 0.2 (20%)

Suppose the Theta for this option is -0.03, meaning the premium decreases by $0.03 per day.

You can calculate the option’s premium (C) at the beginning and after a certain number of days to observe the impact of Theta on the premium.

Tip: Theta, or time decay, is a crucial consideration for options traders. It highlights the importance of time management and selecting appropriate strategies. Options with shorter time to expiration are more sensitive to Theta, so traders should be mindful of their positions and manage them accordingly as expiration approaches.

The Influence of Dividends on Options Pricing

Dividends can have a significant impact on the pricing and behavior of options, particularly for stocks that pay regular dividends. In this article, we’ll explore how dividends influence options pricing and provide mathematical examples to illustrate their effects.

Understanding Dividends and Options

Dividends are periodic payments made by a company to its shareholders. They can affect options in the following ways:

1.  Ex-Dividend Date: When a stock goes ex-dividend (the date on or after which new buyers of the stock are not entitled to the upcoming dividend), the stock price often drops by the amount of the dividend. This drop can impact the pricing of call and put options.
2. Early Exercise: For American-style options, holders may choose to exercise their options early to capture the dividend. This can impact the behavior of options near the ex-dividend date.

Example Calculation

Let’s consider a scenario with the following details:

• Stock price (S): $100
• Strike price (X): $95
• Dividend per share (D): $2
• Time until expiration (T): 30 days
• Risk-free interest rate (rfr): 0.05 (5%)
• Volatility (σ): 0.2 (20%)

Suppose the stock is set to go ex-dividend in 7 days. You can calculate the impact of the expected dividend on the pricing of a call option with the given parameters.

Tip: Understanding the influence of dividends on options pricing is crucial for traders, especially when dealing with dividend-paying stocks. Dividends can affect both the stock price and the behavior of options, particularly those with nearby expiration dates. Traders should be aware of ex-dividend dates and factor in dividend-related considerations when designing their options strategies. consider a call option for stock XYZ with the following parameters:

The Impact of Volatility Skew on Options Trading

Volatility skew refers to the uneven distribution of implied volatility across different strike prices and maturities of options on the same underlying asset. It can have a significant impact on options trading strategies. In this article, we’ll explore the concept of volatility skew and provide mathematical examples to illustrate its influence.

Understanding Volatility Skew

Volatility skew arises when implied volatility differs for options with the same expiration date but different strike prices. It can be categorized as either a positive skew (higher implied volatility for out-of-the-money options) or a negative skew (higher implied volatility for in-the-money options).

Impact on Options Pricing

Volatility skew affects options pricing. Options with higher implied volatility tend to have higher premiums. Traders should be aware of skew when selecting options strategies.

Example Calculation

Let’s consider a scenario with the following details for a stock:

•  Current stock price (S): $50
• Strike price (X): $55
• Time until expiration (T): 60 days
• Risk-free interest rate (r): 0.05 (5%)

Suppose there is a negative volatility skew, with higher implied volatility for in-the-money options. You can calculate the premium of a call option with a strike price of $55 and a put option with the same strike price, given the skew.

Tip: Volatility skew is a critical consideration for options traders, as it can impact the pricing and behavior of options. Traders should be mindful of skew when selecting strike prices and maturities for their options strategies. Understanding how skew affects options pricing can lead to more informed trading decisions.

The Significance of Liquidity in Options Trading

Liquidity is a crucial factor in options trading, impacting everything from execution quality to bid-ask spreads. In this article, we’ll explore the significance of liquidity in options trading and provide mathematical examples to illustrate its importance.

Understanding Liquidity

Liquidity refers to the ease with which an asset can be bought or sold in the market without significantly affecting its price. In options trading, liquidity is essential because it affects trade execution and the costs associated with trading.

Impact on Bid-Ask Spreads

Liquidity influences bid-ask spreads, which are the differences between the highest price a buyer is willing to pay (bid) and the lowest price a seller is willing to accept (ask). In illiquid options, bid-ask spreads tend to be wider, leading to higher trading costs.

Example Calculation

Let’s consider two scenarios:

Scenario 1: An options contract for stock ABC with high liquidity, resulting in a narrow bid-ask spread. Scenario 2: An options contract for the same stock with low liquidity, resulting in a wide bid-ask spread.

You can calculate the trading cost for each scenario based on the bid-ask spread and the number of contracts traded.

Tip: Liquidity is a critical consideration for options traders. High liquidity provides better execution quality and lower trading costs. When selecting options to trade, it’s important to assess the liquidity of the underlying asset and the specific options contract. Additionally, traders should be cautious when trading illiquid options, as wide bid-ask spreads can erode profits.

The Use of Historical Volatility in Options Analysis

Historical volatility is a measure of past price fluctuations in an underlying asset. It can be a valuable tool for options traders when assessing potential future price movements. In this article, we’ll explore the use of historical volatility in options analysis and provide mathematical examples to illustrate its application.

Understanding Historical Volatility

Historical volatility is calculated by measuring the standard deviation of an asset’s past returns over a specific time period. It provides insights into how much an asset’s price has deviated from its average in the past.

Predicting Future Volatility

Options traders often use historical volatility to estimate future price volatility, which can impact the pricing of options. Higher historical volatility may indicate a greater likelihood of significant price movements, potentially affecting the premium of options.

Example Calculation

Let’s consider historical volatility for stock XYZ over the past 30 trading days. You can calculate historical volatility by measuring the standard deviation of daily returns. Using this historical volatility, you can estimate the potential price range for the stock over the next month and assess its impact on options pricing.

Tip: Historical volatility is a valuable tool for options traders, providing insights into an asset’s past price behavior. However, it’s important to remember that historical volatility is not a guarantee of future volatility. Traders should use historical volatility as part of their overall analysis and consider other factors when making trading decisions.

The Role of the VIX Index in Options Trading

The VIX Index, often referred to as the ”fear gauge,” measures market expectations for future volatility. It plays a crucial role in options trading as it can provide insights into market sentiment and potential price movements. In this article, we’ll explore the role of the VIX Index in options trading and provide mathematical examples to illustrate its significance.

Understanding the VIX Index

The VIX Index is calculated based on the implied volatility of options on the S&P 500 Index. It represents the market’s consensus on future volatility and is often used as a gauge of investor fear or complacency.

Using the VIX Index in Options Trading

Options traders often use the VIX Index as a tool for the following purposes:

1.  Market Sentiment: The VIX can indicate whether investors are expecting increased market volatility (higher VIX) or a calmer market (lower VIX).
2. Hedging: Traders can use VIX options and futures to hedge their portfolios against market volatility.

Example Calculation

Suppose the VIX Index is currently at 20, indicating moderate expected volatility. An options trader can use this information to make decisions about their portfolio, such as adjusting position sizes or considering protective strategies.

Tip: The VIX Index is a valuable tool for options traders, providing insights into market sentiment and potential volatility. Traders should monitor the VIX regularly and use it as part of their overall analysis when making trading decisions. It’s essential to understand that the VIX is not a directional indicator but rather a measure of expected future volatility.

The Impact of Interest Rates on Options Pricing

Interest rates play a crucial role in options pricing, particularly when calculating the present value of future cash flows. In this article, we’ll explore how interest rates influence options pricing and provide mathematical examples to illustrate their impact.

Understanding Interest Rates and Options Pricing

Interest rates affect options pricing through the present value concept. The higher the interest rate, the more valuable it is to receive cash flows sooner rather than later. This principle applies to both call and put options.

Impact on Options Premium

Higher interest rates tend to result in lower call option premiums and higher put option premiums. This is because the present value of potential future gains for call options is reduced, while the present value of potential future losses for put options is increased.

Example Calculation

Let’s consider a call option for stock ABC with the following parameters:

•  Current stock price (S): $50
• Strike price (X): $55
• Time until expiration (T): 1 year
• Risk-free interest rate (r): 0.1 (10%)
• Volatility (σ): 0.2 (20%)

You can calculate the impact of the interest rate (r) on the premium of the call option using the Black-Scholes model.

Tip: Interest rates are a critical factor in options pricing, and options traders should be mindful of their impact. Changes in interest rates can affect the attractiveness of various options strategies and may influence trading decisions. Understanding the relationship between interest rates and options pricing is essential for successful trading.

The Role of Options Expiration in Trading Strategies

Options expiration is a critical factor that significantly influences trading strategies. Understanding how it impacts different options positions is essential for effective options trading. In this article, we’ll explore the impact of options expiration on four common options strategies: long call, short call, long put, and short put, and provide mathematical examples to illustrate their significance.

Long Call

A long call position involves buying a call option with the expectation that the underlying asset’s price will rise. As options approach expiration, their time value decreases, which can impact the long call strategy. Let’s consider an example:

•  Stock ABC’s current price (S): $50
• Strike price (X): $55
• Time until expiration (T): 30 days
• Risk-free interest rate (r): 0.05 (5%)

As expiration nears, the time value of the long call option decreases, affecting its premium. Traders need to assess whether to exercise the option, sell it, or let it expire based on market conditions.

Short Call

A short call position involves selling a call option with the obligation to sell the underlying asset if the option is exercised. As expiration approaches, short call writers must monitor their position carefully. Here’s an example:

•  Stock DEF’s current price (S): $60
• Strike price (X): $55
• Time until expiration (T): 20 days
• Risk-free interest rate (r): 0.04 (4%)

As expiration nears, the risk of the short call being exercised increases. Short call writers may need to take actions such as buying back the option to close the position or managing it through other means.

Long Put

A long put position involves buying a put option with the expectation that the underlying asset’s price will decline. As options near expiration, their time value can decrease or increase, depending on market conditions. Let’s consider an example:

•  Stock GHI’s current price (S): $70
• Strike price (X): $65
• Time until expiration (T): 40 days
• Risk-free interest rate (r): 0.03 (3%)

If the stock’s price doesn’t move significantly, the long put’s time value may erode as expiration approaches. Traders need to assess their options for managing the position.

Short Put

A short put position involves selling a put option with the obligation to buy the underlying asset if the option is exercised. As expiration nears, short put writers must monitor their position closely. Here’s an example:

•  Stock JKL’s current price (S): $45
• Strike price (X): $50
• Time until expiration (T): 10 days
• Risk-free interest rate (r): 0.06 (6%)

As expiration approaches, the short put’s risk increases, as the option may be exercised. Short put writers may consider strategies like rolling the position or buying back the option to close it.

Tip: Options expiration can significantly impact the profitability and risk of options positions. Traders should have a clear understanding of how time decay affects their strategies and monitor their positions as expiration dates approach. Additionally, having a plan for managing options nearing expiration is essential for successful options trading

Using the Put-Call Parity in Options Trading

Put-call parity is a fundamental concept in options trading that relates the prices of call and put options with the same strike price and expiration date. Understanding put-call parity can help traders identify arbitrage opportunities and make informed decisions. In this article, we’ll explore the concept of put-call parity and provide mathematical examples to illustrate its application.

Understanding Put-Call Parity

Put-call parity states that the sum of the present values of a European call option and a European put option with the same strike price (X) and expiration date (T) should equal the current stock price (S) plus the present value of the strike price. Mathematically, it can be expressed as:

Where:

•  C = Call option price
• P = Put option price
• S = Current stock price
• X = Strike price
• r = Risk-free interest rate
• T = Time until expiration

Application in Options Trading

Traders can use put-call parity to:

1. Identify Arbitrage Opportunities: If put-call parity is violated, it can create arbitrage opportunities. Traders can take advantage of these mispricing to make risk-free profits.
2. Price Options: Put-call parity can be used to calculate the price of one type of option based on the price of the other type, helping traders assess fair values.

Example Calculation

Let’s consider the following scenario:

•  Stock ABC’s current price (S): $60
• Strike price (X): $55
• Time until expiration (T): 0.5 years
• Risk-free interest rate (r): 0.05 (5%)
• Call option price (C): $8
• Put option price (P): $5

We can use put-call parity to verify if the prices of the call and put options adhere to the parity equation.

Tip: Put-call parity is a crucial concept in options trading that helps ensure consistency in option prices. Traders should be aware of this principle to identify opportunities for arbitrage and assess the fairness of option prices. Monitoring deviations from put-call parity can be a valuable part of a trader’s toolbox.

The Role of Implied Volatility in Options Strategies

Implied volatility is a critical component of options pricing and trading strategies. It represents the market’s expectations for future price volatility of the underlying asset. In this article, we’ll explore the role of implied volatility in options strategies and provide mathematical examples to illustrate its significance.

Understanding Implied Volatility

Implied volatility is a measure of expected future price swings. When implied volatility is high, options tend to have higher premiums, reflecting the uncertainty in the market. Conversely, low implied volatility results in lower option premiums.

Impact on Options Strategies

Implied volatility plays a crucial role in options strategies. Here are some examples of how it can affect different strategies:

1.  Buying Options: Traders may buy options when they expect implied volatility to increase, as this can boost option prices.
2. Selling Options: Option sellers may benefit from high implied volatility because it leads to higher premiums. However, they should be cautious when volatility is low.

Example Calculation

Let’s consider an example involving a call option for stock XYZ with the following details:

•  Current stock price (S): $50
• Strike price (X): $55
• Time until expiration (T): 60 days
• Risk-free interest rate (r): 0.04 (4%)

Suppose the implied volatility for this option is 0.3 (30%). You can calculate the option’s premium (C) based on this implied volatility.

Tip: Implied volatility is a crucial factor for options traders to consider when designing their strategies. Traders should assess their outlook on volatility and use it as a key input when evaluating potential trades. Understanding how implied volatility impacts options pricing is essential for successful options trading.